Performance Enhancements

Caveat: Factors specified on this page are obtained from micro-benchmarks performed on specific primitive functions; in real applications factors will depend on a mix of primitives.

All benchmark tests were performed on 64-bit interpreters on Linux/Microsoft Windows operating systems.

Internal Benchmarks

Internal benchmarking was performed on the initial release of Dyalog version 17.0 and the results compared with the initial release of Dyalog version 16.0.

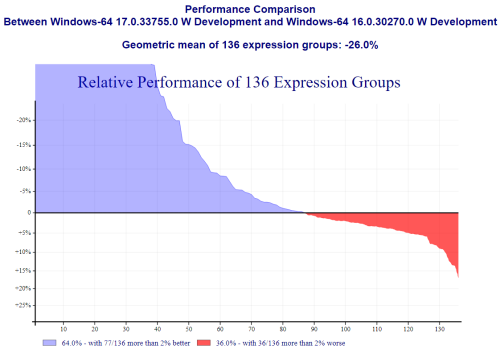
The benchmarking process comprises over 13,000 benchmarks in more than 130 groups; the group geometric mean timing ratios are measured and plotted against the groups sorted by their means. The vertical axis of the graph shows the ratios as a percentage change; negative values are shown in blue and indicate a performance enhancement, and positive values are shown in red and indicate a deterioration in performance.

Results showed that core interpreter performance in Dyalog version 17.0 has an average improvement of 26% over Dyalog version 16.0.

Areas of Focus

For previous releases we have presented the ways in which Dyalog has been sped up in tabular form. We tried to make such a table for this release, and all the improvements wouldn’t fit! Dyalog version 17.0 has been the subject of several broad classes of improvements, as well as dozens of special cases and specific speedups. Here’s an overview of what’s changed:

Vector instructions – Dyalog version 17.0 massively increases the use of vector instructions both in terms of the supported platforms and the operations that are vectorised. Performance gains are huge in some cases, for example, comparing vectors of one-byte integers is 13.5 times faster in version 17.0 than in version 16.0 on modern Intel hardware.
Simplifications – Many operations have special cases in which they are equivalent to less expensive operations. For example, 0+⍵ is just ⍵, and 0×⍵ is an array of zeroes. Using the more efficient operation (sometimes known as strength reduction) can speed up programs that require the generality of the first operation but usually only use the second. In Dyalog version 17.0, many simpler cases that can occur in scalar dyadics and set functions have been identified and are now supported by special code.
Boolean operations – Many existing optimisations for Boolean operations have been extended with more complete, fast, implementations of Boolean scalar dyadics, reductions, scans, inner products and outer products.
Replicate and related functions – Replicate (dyadic /), expand (dyadic \), and where (monadic ⍸) have been significantly reworked, not only increasing their speed in common cases but also making them less reliant on branch prediction (which can result in varying and machine-dependent performance).

Some specific examples of improvements follow. Measurements are taken on an Intel Kaby Lake i7-7500U, which is a fairly new, high-end machine. While a small number of improvements are Intel-specific, the measurements below should be representative of what you might see. The tests were performed on long arrays (usually a million elements); substantial improvements can usually be seen with as few as 20 elements, and the full speed-up is usually apparent with 1,000 elements.

Vector Instructions

Dyalog version 17.0 greatly expands the use of vector instructions and makes their use much more consistent. The more advanced AVX instructions on x86 are now supported, and use of IBM’s VMX instructions has been extended so that POWER architectures use vector instructions as often as x86 ones. Support for ARM’s NEON vector instruction set has been added so that Raspberry Pis with vector units (Pi 2 and later) can use vector instructions. The most common operations were vectorised in Dyalog version 16.0, but cases where these optimisations didn’t apply, or where AVX2 offers an improvement, are quite common. In Dyalog version 17.0:

Taking the maximum of one vector of 1-byte integers and another of 2-byte integers is now 3.8x faster.
Dividing a vector of 2-byte integers by another such vector is 4.5x faster.
Taking the 0.5th power (square root) of a floating-point vector is now 4.7x faster.
Adding a vector of Booleans to another vector of 1-byte integers is 5.2x faster.

More special cases are now recognised by scalar dyadics. Every scalar dyadic except + × * ○ now has special code when both of its arguments are the same array, and the operations X+0, X-0, X×1, X÷1, 0|Y, X*1, X×0 and X*0 (irrespective of exact syntax and including reversals for commutative functions) are all handled with fast code. In addition:

Dividing a floating-point array by itself is now 179x faster.
Taking the first power of an array now takes a constant 60 nanoseconds.

Comparisons

Although vector instructions have a big impact on arithmetic, they are even more effective when used for comparisons. Comparisons between arrays of the same type have been sped up by the following factors:

	1-byte	13x
	2-byte	4.7x
	4-byte	1.6x
	floating-point	1.7x
	decimal floating-point	2.0x

(Decimal floats don’t use vector instructions, but we sped them up anyway!) Outer products also benefit greatly: computing a shape 1000 1000 identity matrix using ∘.=⍨⍳1e3 is now 13.9x faster, without any identity-specific code. We took the opportunity to add a few tricks when the result of the comparison can be determined from argument types:

Comparing a vector of 2-byte integers with a scalar number outside of 2-byte range is 133x faster
If the scalar number is positive, then taking the minimum of these two arrays is now instantaneous (a constant 60 nanoseconds)
Testing for equality between 1-byte integers and 1-byte characters is 209x faster

Indexing

Indexing has seen a substantial amount of work in Dyalog version 17.0. Selection from a very short array is a highlight:

Indexing the rows of a shape 2 17 Boolean matrix by a Boolean vector is now 55x faster.
Taking the outer product (∘.≠) of a length 1e4 Boolean vector with a length 7 Boolean vector is 22x faster.
Selecting from up to 128-⎕IO Boolean values using a short-integer index vector is now 13x faster. That includes selecting from each row of a Boolean matrix. On a matrix it’s 18x faster than before.
Selecting from up to 16-⎕IO 1-byte values using a short-integer index vector is now 2.7x faster.

Replicate (/), Expand (\), and Where (⍸)

These functions have been the targets of extensive optimisation. The most improved cases are those that have a small-type right argument, a scalar left argument and a sparse argument to ⍸ or a left argument to / or \ that changes value from 0 to 1 or back few times (much more common than it sounds). For example:

Compress (replicate with a Boolean left argument) on 1-byte values is 11x faster.
Compress on 2-byte values is 6.1x faster.
Replicate on a Boolean vector is about 2x faster, depending on the values in the left argument.
The scalar replicate 4/ on 2-byte values is about 2.5x faster. Other types and constants benefit as well.
The outer product (∘.+) uses replicate when the right argument is small enough. With a right argument of 5 short integers, it’s 2.8x faster.
Where with a sparse argument consisting of a million values with one out of every hundred set is 6.1x faster.

Miscellaneous

We told you there were too many to list…

Reversing the rows of a shape 1e4 13 matrix of 1-byte data is 1.8x faster.
The reduction ∧⌿ on a shape 1e4 12 Boolean matrix is at least 3.5x faster, but can finish early and be up to 53x faster.
Minus reduction (-/) on a Boolean array is up to 1,460x faster.
Converting integers to characters with ⎕UCS is 11.2x faster, and in the other direction it’s 12.7x faster.
Match each (≡¨) and its negation (≢¨) are 5.8x faster on vectors of short vectors.