A Memo Operator

Abstract
Some functions are simply stated and easily understood as multiply-recursive functions. For example, the Fibonacci numbers are {1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}. A drawback of multiple recursion is abysmal performance even for moderate-sized arguments, consequently motivating resorts to circumlocutions. The memo operator addresses the performance problem and restores multiple recursion to the toolkit of thought. We present a memo operator modelled as a 6-line d-operator.
⎕io←0 throughout.
The Man Who Knew Infinity
Jay sent out an e-mail asking who would be interested to go see the film The Man Who Knew Infinity. Fiona’s response: “Ah, Mr. 1729; I’m in.” John was game, and so was I.
The Number of Partitions
Nick found an essay by Stephen Wolfram on Ramanujan written on occasion of the film, wherein Wolfram said:

In[1]:= PartitionsP[200]
Out[1]= 3 972 999 029 388

A partition of a non-negative integer n is a vector v of positive integers such that n = +/v, where the order in v is not significant. For example, the partitions of the first seven non-negative integers are:

┌┐
││
└┘
┌─┐
│1│
└─┘
┌─┬───┐
│2│1 1│
└─┴───┘
┌─┬───┬─────┐
│3│2 1│1 1 1│
└─┴───┴─────┘
┌─┬───┬───┬─────┬───────┐
│4│3 1│2 2│2 1 1│1 1 1 1│
└─┴───┴───┴─────┴───────┘
┌─┬───┬───┬─────┬─────┬───────┬─────────┐
│5│4 1│3 2│3 1 1│2 2 1│2 1 1 1│1 1 1 1 1│
└─┴───┴───┴─────┴─────┴───────┴─────────┘
┌─┬───┬───┬─────┬───┬─────┬───────┬─────┬───────┬─────────┬───────────┐
│6│5 1│4 2│4 1 1│3 3│3 2 1│3 1 1 1│2 2 2│2 2 1 1│2 1 1 1 1│1 1 1 1 1 1│
└─┴───┴───┴─────┴───┴─────┴───────┴─────┴───────┴─────────┴───────────┘

Can we compute the partition counting function “instantaneously” in APL?
We will use a recurrence relation derived from the pentagonal number theorem, proved by Euler more than 160 years before Hardy and Ramanujan:

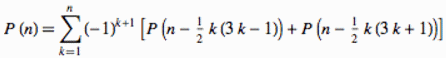
equation (11) in http://mathworld.wolfram.com/PartitionFunctionP.html. In APL:

      pn  ← {0≥⍵:0=⍵ ⋄ -/+⌿∇¨rec ⍵}
      rec ← {⍵ - (÷∘2 (×⍤1) ¯1 1 ∘.+ 3∘×) 1+⍳⌈0.5*⍨⍵×2÷3}
      pn¨0 1 2 3 4 5 6
1 1 2 3 5 7 11
      pn 30
5604

Warning: don’t try pn 200 because that would take a while! Why? pn 200 would engender pn being applied to each element of rec 200 and:

   rec 200
199 195 188 178 165 149 130 108 83 55 24 ¯10
198 193 185 174 160 143 123 100 74 45 13 ¯22

Each of the non-negative values would itself engender further recursive applications.
A Memo Operator
I recalled from J the memo adverb (monadic operator) M. Paraphrasing the J dictionary: f M is the same as f but may keep a record of the arguments and results for reuse. It is commonly used for multiply-recursive functions. Sounds like just the ticket!
The functionistas had previously implemented a (dyadic) memo operator. The version here is more restrictive but simpler. The restrictions are as follows:

• The cache is constructed “on the fly” and is discarded once the operand finishes execution.
• The operand is a dfn {condition:basis ⋄ expression} where none of condition, base and expression contain a ⋄ and recursion is denoted by ∇ in expression
• The arguments are scalar integers.
• The operand function does not have ¯1 as a result.
• A recursive call is on a smaller integer.

With these restrictions, our memo operator can be defined as follows:

M←{
 f←⍺⍺
 i←2+'⋄'⍳⍨t←3↓,⎕CR'f'
 0=⎕NC'⍺':⍎' {T←(1+  ⍵)⍴¯1 ⋄  {',(i↑t),'¯1≢T[⍵]  :⊃T[⍵]   ⋄ ⊃T[⍵]  ←⊂',(i↓t),'⍵}⍵'
          ⍎'⍺{T←(1+⍺,⍵)⍴¯1 ⋄ ⍺{',(i↑t),'¯1≢T[⍺;⍵]:⊃T[⍺;⍵] ⋄ ⊃T[⍺;⍵]←⊂',(i↓t),'⍵}⍵'
}
      pn M 10
42
      pn 10
42

Obviously, the ⍎ lines in M are crucial. When the operand is pn, the expression which is executed is as follows; the characters inserted by M are shown in red.

{T←(1+⍵)⍴¯1 ⋄ {0≥⍵:0=⍵ ⋄ ¯1≢T[⍵]:⊃T[⍵] ⋄ ⊃T[⍵]←⊂-/+⌿∇¨rec ⍵}⍵}⍵

The machinations produce a worthwhile performance improvement:

      pn M 30
5604
      cmpx 'pn M 30'
3.94E¯4
      cmpx 'pn 30'
4.49E1
      4.49e1 ÷ 3.94e¯4
113959

That is, pn M 30 is faster than pn 30 by a factor of 114 thousand.
Can APL compute pn M 200 “instantaneously”? Yes it can, for a suitable definition of “instantaneous”.

      cmpx 'm←pn M 200'
4.47E¯3
      m
3.973E12
      0⍕m
 3972999029388

M also works on operands which are anonymous, dyadic, or have non-scalar results.
Fibonacci Numbers

   fib←{1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}
   fib¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
   fib M¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
   cmpx 'fib 30'
1.45E0
   cmpx 'fib M 30'
1.08E¯4

Anonymous function:

      {1≥⍵:⍵ ⋄ (∇ ⍵-2)+∇ ⍵-1}M¨ ⍳15
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

Combinations
⍺ comb ⍵ produces a matrix of all the size-⍺ combinations of ⍳⍵. The algorithm is from the venerable APL: An Interactive Approach by Gilman and Rose.

      comb←{(⍺≥⍵)∨0=⍺:((⍺≤⍵),⍺)⍴⍳⍺ ⋄ (0,1+(⍺-1)∇ ⍵-1)⍪1+⍺ ∇ ⍵-1}
      3 comb 5
0 1 2
0 1 3
0 1 4
0 2 3
0 2 4
0 3 4
1 2 3
1 2 4
1 3 4
2 3 4
      3 (comb ≡ comb M) 5
1
      cmpx '8 comb M 16' '8 comb 16'
  8 comb M 16 → 1.00E¯3 |     0% ⎕
  8 comb 16   → 3.63E¯2 | +3526% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

A faster comb is possible without a memo operator, but it’s not easy. (See for example section 4.1 of my APL87 paper.) A memo operator addresses the performance problem with multiple recursion and restores it to the toolkit of thought.
Presented at the BAA seminar at the Royal Society of Arts on 2016-05-20